Analysis: recent events highlight how difficult it is to achieve a safe ('soft') and successful lunar landing, but without it, all else fails
Man walking on the moon was among the greatest achievements of the 20th century for humankind. The resources and expertise employed in the lunar landing programme were extraordinary, and of a level not typically seen outside of war-time. Indeed, the first lunar walk took place in the context of an ideological war: the Cold War. The intensity of efforts directed towards achieving a crewed moon-landing were reminiscent of the Manhattan project which developed the atomic bomb.
However, both of these projects could not have been more fundamentally different in their objectives: whereas the Manhattan project was almost exclusively destructive in its aims, the moon-landing project was constructive, forward-looking, and chosen by John F. Kennedy to be an endeavour that would capture the public imagination, and prove the US' world leadership in this ambitious scientific field.
In order for man to walk on the moon, man first needed to reach, and land safely on, the moon. This simplistic statement belies a myriad of potential difficulties and challenges from both the scientific and technological (space-craft), and physiological and psychological (human), sides which needed to be overcome.
We need your consent to load this rte-player contentWe use rte-player to manage extra content that can set cookies on your device and collect data about your activity. Please review their details and accept them to load the content.Manage Preferences
From RTÉ Archives, US astronauts Neil Armstrong, Buzz Aldrin and Michael Collins give a news conference ahead of the launch of the Apollo 11 (RTÉ News report broadcast 16 July 1969)
The human dimension to moon-landing is the most glamorous and exhilarating. Immortality was bestowed immediately upon the first crew of astronauts to successfully achieve a lunar landing, and Neil Armstrong's "One small step…" declaration is writ large in the legend of human achievement. The courage, resilience and skill required to firstly undertake such a fraught journey, and to then leave the safety of the landing module to walk on the unknown lunar landscape, is truly extraordinary. It is therefore not surprising that the first candidates for astronauts selected by NASA consisted exclusively of elite army test pilots.
However, in contrast to the derring-do and heroism associated with fighter pilots, it is often overlooked that the first crewed space-flights involved monkeys and other primates. Chimpanzees coped admirably well with being thrusted into outer space, and remained sufficiently calm and well-behaved in outer space not to jeopardise their successful return to Earth. The curiously similar outcomes between fighter heroes, and apes, in these pioneering crewed space-missions (which is archly documented in Tom Wolfe’s classic book The Right Stuff) reflects the fact that large portions of space-travel requires very little input from the passengers; rather, science and technology determine and control the vast majority of the intricate processes involved.
From the technological point of view, nearly any lay person (particularly those having even brief encounters with science fiction) can imagine numerous major challenges and hazards involved with executing a successful moon-landing, such as: achieving a successful (non-explosive!) launch of the spacecraft; escaping from the Earth's atmosphere into the outer reaches of space; the successful detachment of the lunar module from the command module; and finally effecting a safe landing on the moon. This final aspect of the process is often taken for granted and overlooked, probably because safety in any aspect of life is rarely spectacular, and hence fails to capture the human imagination. However, without a safe ("soft") moon-landing, all else fails. Indeed, recent events of the past few weeks highlight how difficult, and important, it is to achieve a successful soft lunar descent.
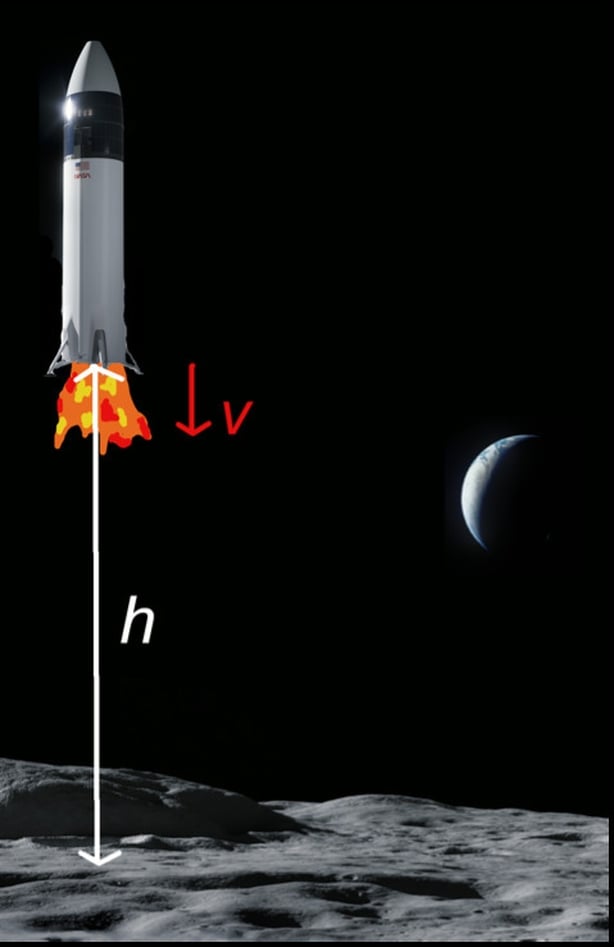
The issue of achieving a safe lunar-landing is a highly complex and multi-faceted problem but, at its essence, it can be expressed in terms of a deceptively simple mathematical formulation which is perplexingly difficult to analyse. Essentially, the lunar module needs not just to reach the surface of the moon ("to land") but, more importantly, it should arrive at the lunar surface without crashing ("soft landing"). A simplified model of a lunar landing is represented by the schematic above, where we assume that the physical terrain beneath the lunar module is flat.
Suppose the lunar module is located at a height (h) directly above the lunar surface, and moving with a speed (v) vertically downwards towards the lunar surface. The moon's gravitational force (which is approximately 1/6th that of the Earth) is attracting the module downwards, and this serves to increases the downward velocity of the module. In order to counteract this downward force, the lunar module must deploy its rockets. The aim is to control this upward thrust in such a way that the module reaches the lunar surface (where h=0) with a velocity that is precisely zero (with v=0).
This is a simple enough problem to describe up to this point. One coarse but somewhat intuitive approach to ensuring that a lunar module lands "softly" might employ several rocket bursts which enables the lunar module to gradually approach the surface by alternating between ever-decreasing downward and upward motions. This would be the lunar analogue of parallel parking into a tight space by repeatedly driving in-and-out, making small adjustments to the steering each time, until finally getting it right. However this unsophisticated approach would be wasteful of fuel, whereas minimising the weight of a space craft, and the fuel it consumes in any mission, are inter-linked constraints which are of primary importance. Therefore, when designing a soft-moon landing problem it is vital to minimise the fuel consumed. Solving the moon-landing problem in so that that v=0 when h=0, and in such a way that minimises the consumption of fuel, can be achieved by employing a sophisticated branch of mathematics called optimal control theory.
We need your consent to load this rte-player contentWe use rte-player to manage extra content that can set cookies on your device and collect data about your activity. Please review their details and accept them to load the content.Manage Preferences
From RTÉ Radio 1's Ray D'Arcy Show, Kevin Nolan, Lecturer in Physics at TU Dublin and PhD candidate in Space Science at MTU, talks about the Indian mission to the Moon
Control theory is a broad discipline at the interface of mathematics and engineering which has many uses throughout modern applications. Surprisingly, given its potential for describing extremely complex phenomena, control theory is not just an esoteric branch of mathematics or engineering: it is something we employ automatically in all aspects of our life without a conscious awareness of it. For example, our body naturally tries to regulate (or "control") its breathing-rate, heartbeat, temperature, and so on, when these vital processes deviate from their resting states due to shock, or other external factors.
A less natural but elementary example of control theory can be found in the act of balancing a sweeping-brush upright at the end of one's finger. When the brush is perfectly upright, it is in equilibrium. However, this is not a stable equilibrium since any tiny perturbation of the brush will soon result in it falling over. When we observe the brush moving, we intuitively adjust our hand sideways to counteract the falling motion, and in this fashion the "upright brush routine" can be maintained for an extended amount of time by controlling how we move our hand. This type of control, which uses information on the current state of things (that is, which way the brush is falling) to guide how we control our subsequent reaction (that is, which way we move our hand) is called a feedback control.
From DW, Russia's lunar lander Luna-25 crashes into moon
Control theory has been a feature of engineering design through the ages, with a prominent early example of feedback control in design engineering being the Watt governor in steam engines in the 1700s. However the optimal control theory that is required to solve the soft moon-landing problem is much more recent. The mathematical development of optimal control theory was initiated in the mid-20th century, largely by the brilliant and controversial Russian mathematician Lev Pontryagin.
The soft-moon landing problem is complicated even further due to its time varying and, more importantly, nonlinear nature. The mass of the space module varies with time, since engine thrusts consume fuel, thereby reducing the overall body mass. The acceleration of the space craft depends linearly on the engine thrust, but nonlinearly on the mass of the lunar module. The nonlinear nature of this problem means that it is intractable to mathematical analysis alone, and its solution requires an interplay between highly sophisticated mathematical theory, and modern computational analysis.
In spite of these complications, recent events have dramatically demonstrated how important and necessary it is to achieve a successful soft lunar descent.
The views expressed here are those of the author and do not represent or reflect the views of RTÉ




