Analysis: mathematics provides models that describe what happens in our brains when we make decisions about what to do
By John Butler and Rebecca Brady, TU Dublin
Decision-making is a constant part of our day to day lives, and neuroscientists have delved into how our brains handle such choices. They investigate the behaviour and brain regions involved in the decision-making process. However, experimental neuroscience alone is not enough to understand the decision-making processes. Mathematics comes into play by providing models that describe these processes.
Should I stay or should I go?
Have you ever found yourself sitting in your favourite pub pondering a decision like The Clash? How would an applied mathematician approach the situation of deciding whether to stay and have another pint or to go home and call it a night?
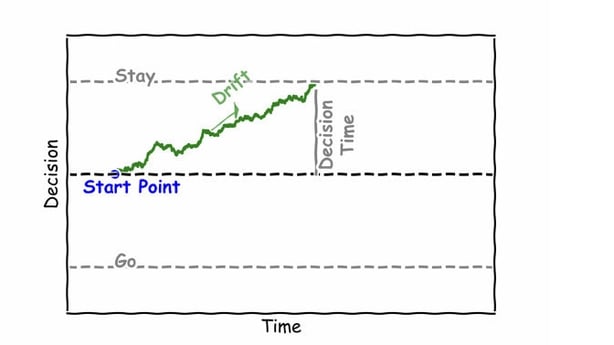
Initially, the mathematician would consider various factors and attempt to simplify the situation. Time becomes a crucial element, with a certain duration allocated for decision-making. A mathematician would visualise this on a graph with time represented on the x-axis, and the accumulated evidence for the decision shown on the y-axis.

At the beginning of the decision-making process and assuming you're undecided about that next drink, you must gather and accumulate information before making a choice. Mathematically, we model the speed of accumulation using a parameter called the drift rate, mu (μ). Reasons (evidence) to stay like good chat and a nice pint, make this positive, while reasons to go (like a bad pint or the siren call of the chipper) make this negative.
However, this representation only accounts for two dimensions and of course there is noise (moment to moment variability) in the decision process which is accounted for by the parameter sigma (σ). Of course, in decision-making we don't accumulate information indefinitely - at some point we judge that we have enough information to commit to a decision. Mathematically, we bring in this "stop when enough" mechanism by introducing thresholds or "bounds"—with a top bound representing the choice to stay and a bottom bound representing the choice to go.
At the start of the decision-making process, we find ourselves somewhere between these two bounds and, as we accumulate evidence, the graph begins to take shape. Once the evidence reaches either the stay or go bound, the decision is made and we know the decision time - which can tell us a lot about the decision process. This mathematical framework enables us to think about simple decision-making processes, where information is gathered over time, providing evidence that guides us toward choosing to either stay or go.
Change your mind
But what happens if you change your mind, and how does that look mathematically? Consider sitting in the pub, contemplating whether to stay or go. You're observing your surroundings, assessing your feelings, and leaning towards going home due to tiredness or other obligations - negative influences on our drift rate μ.
Suddenly, you notice that the Champions League finals is on the TV and you have an excellent seat. This change in information alters your decision-making process, with these positive influences on drift driving it toward Staying. In mathematical terms, this would involve a sudden change in the graph, reflecting the updated information, causing the process to turn around, rescued from a surely disastrous near decision to Go. While the function itself may remain the same, it is the incoming information that influences the decision.

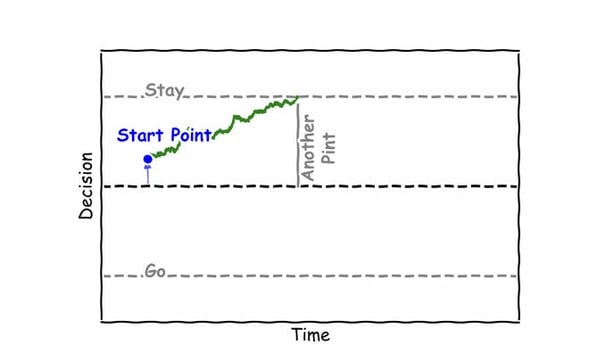
Let's have another drink
Let's think about having a second drink at the pub. If you've already had one drink, you are more likely to have another. How would a mathematician think about this? One approach would be to adjust the starting point. Instead of beginning midway between Stay and Go, you may already be biased toward Staying, shifting the starting point further up. Again, this seemingly simple adjustment in mathematical terms represents a significant change in the decision-making outcome.
An Irish goodbye
Consider a friend who abruptly decides to leave the pub without saying goodbye, known in America as "An Irish goodbye". How could we model this mathematically? As mentioned earlier, there are thresholds or bounds that determine decision-making outcomes. Due to various reasons, these thresholds may decrease which results in faster but less accurate decisions which is known as a speed accuracy trade-off.
For instance, if someone has consumed too many drinks, their decision-making threshold might be lowered. This change in threshold can result in abrupt decisions that are close to a 50/50 chance to Stay for another drink or to Go home, both appearing as sudden choices.

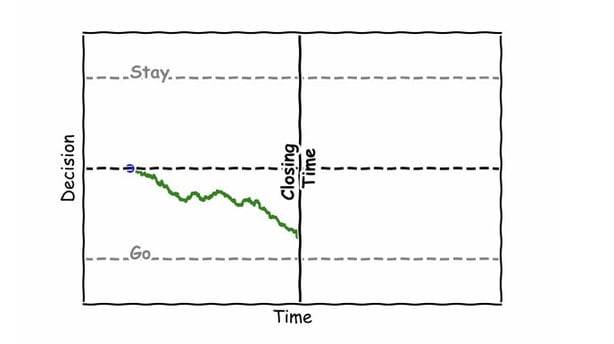
Closing time
Closing time at the pub is another interesting scenario. If you're taking too long to decide, closing time intervenes, making the decision for you. Mathematically, we simply introduce a stop point, overriding any further accumulation of information. Regardless of how much evidence is accumulated, the option to stay or go is eliminated—you must go.
All these factors—drift rate μ (speed of decision-making), noise in decision-making σ, decision time step dt, decision threshold bounds, and starting point—can be used to model decision-making. Combining these factors, researchers have developed the drift diffusion model, a mathematical equation that describes and models the rate of change of the decision-making process 'x' and is written like this:
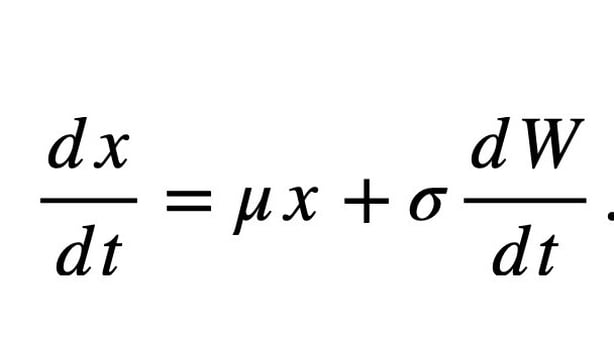
This equation says that the rate of change of decision is related to the current decision direction and some noise (variability). The equation transforms a seemingly mundane experience into a realm where our brains engage in complex mathematical computations.
In fact, evidence suggests that these mathematical models closely align with how our brains actually make decisions. Competing brain regions exist for the choices of staying or leaving, influencing the decision-making circuits. One region promotes the decision to stay, the other encourages going and these regions exert opposing effects on the decision-making process.
Consequently, the mathematical modelling closely corresponds to the intricate decision-making processes occurring in our brains. This applies not only to simple decisions like whether to have another drink but also to more significant choices we encounter in our lives. So, the next time you find yourself at a pub, contemplating whether to stay or go, remember that your brain is engaging in intricate mathematical computations.
This article is based on a Pint of Science talk given by Dr John Butler in 2022. It was also adapted into a virtual escape room for kids where the question was, "will I walk or cycle to school?". This is available in Arabic, Chinese, English, French, Hebrew and Spanish
Dr John Butler is a mathematics lecturer at TU Dublin who uses mathematics and neuroscience to design experiments and analysis methods to understand how the brain uses vision, touch, hearing, and body motion information. Rebecca Brady is a mathematics PhD student at TU Dublin. She is an Irish Research Council awardee.
The views expressed here are those of the author and do not represent or reflect the views of RTÉ


